数学学法指导三例
例一 多向考虑解法多 【题目】
张叔叔因为身体不好在家休息，这期间的天气状况是：（1）上午和下午一共下了7次雨；（2）有5个下午是晴天；（3）有6个上午是晴天；（4）如果下午下雨，整个上午是晴天。请问，张叔叔一共休息了多少天？
【分析与解】
如果从不同角度思考，可以得到不同的解法。
解法一：列表法。通过尝试调整，最后列出如下符合题目要求的表格： 
所以，张叔叔一共休息了9天。 解法二：数量关系法。因为这期间的天气只有雨天和晴天两种情况，我们可以得出数量关系：雨天的天数＋晴天的天数＝一共休息的天数。根据条件（1）可求出雨天天数为：7÷2＝3.5（天）；根据条件（2）和（3）可以求出晴天天数为：（5＋6）÷2＝5.5（天）。所以，张叔叔一共休息天数为：3.5＋5.5＝9（天） 解法三：假设法。假设这期间每天都是半天晴天，半天雨天。这样，根据条件（1）推出共休息了7天，其中晴天为7个半天。这与已知条件（2）、（3）共有（5＋6）11个半天是晴天相比，少算了（11－7）4个半天，也就是2天。所以，总天数应该比7天还要多2天，即7＋2＝9（天）。
例二 巧转化妙解题 【题目】
如下图，长方形ABCD的长AB＝5厘米，宽BC＝4厘米，三角形COE的面积比三角形DOA的面积小5平方厘米，求CE的长。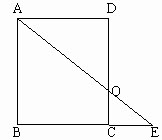 
【分析与解】
因长方形ABCD与三角形BAE共用了梯形ABCO，故三角形DOA的面积与三角形COE的面积差就等于长方形ABCD的面积与三角形BAE的面积差。已知三角形COE的面积比三角形DOA的面积小5平方厘米，也就是说三角形BAE的面积比长方形ABCD的面积小5平方厘米。由于长方形ABCD的面积为（4×5）20平方厘米，因此三角形BAE的面积为（4×5－5）15平方厘米，则BE＝15×2÷5＝6（厘米），故CE＝6－4＝2（厘米）。
例三 善思出巧解 【题目】工程队计划用30天修一条长2400米的公路，修了6天后，又增加了一批工人一起工作，这样修路的速度是原来的2倍。修完这条公路还需要多少天？ 【一般解法】要求修完这条公路还需要多少天，应先算出修了6天后还剩下多少米，以及现在每天修路多少米。根据题意：还剩下的米数为1920 （米），现在每天修的米数为：2400÷30×2=160（米），修完这条公路还需要的天数为：1920÷160=12（天）。综合算式为（2400－2400÷30×6）÷（2400÷30×2）=12（天） 【巧妙解法】如果修路的速度不加快，那么修了6天后，余下的任务还要修（30－6）24天。根据“（现在）修路的速度是原来的2倍”得出：修同样的路，现在所用的时间只要原来的一半，所以，修完这条公路还需要的时间是：（30－6）÷2=12（天）。
